난이도

Gold 5

문제

자두는 자두를 좋아한다. 그래서 집에 자두나무를 심어두고, 여기서 열리는 자두를 먹고는 한다. 하지만 자두는 키가 작아서 자두를 따먹지는 못하고, 자두가 떨어질 때까지 기다린 다음에 떨어지는 자두를 받아서 먹고는 한다. 자두를 잡을 때에는 자두가 허공에 있을 때 잡아야 하는데, 이는 자두가 말랑말랑하여 바닥에 떨어지면 못 먹을 정도로 뭉개지기 때문이다.

매 초마다, 두 개의 나무 중 하나의 나무에서 열매가 떨어지게 된다. 만약 열매가 떨어지는 순간, 자두가 그 나무의 아래에 서 있으면 자두는 그 열매를 받아먹을 수 있다. 두 개의 나무는 그다지 멀리 떨어져 있지 않기 때문에, 자두는 하나의 나무 아래에 서 있다가 다른 나무 아래로 빠르게(1초보다 훨씬 짧은 시간에) 움직일 수 있다. 하지만 자두는 체력이 그다지 좋지 못해서 많이 움직일 수는 없다.

자두는 T(1≤T≤1,000)초 동안 떨어지게 된다. 자두는 최대 W(1≤W≤30)번만 움직이고 싶어 한다. 매 초마다 어느 나무에서 자두가 떨어질지에 대한 정보가 주어졌을 때, 자두가 받을 수 있는 자두의 개수를 구해내는 프로그램을 작성하시오. 자두는 1번 자두나무 아래에 위치해 있다고 한다.

입력

첫째 줄에 두 정수 T, W가 주어진다. 다음 T개의 줄에는 각 순간에 자두가 떨어지는 나무의 번호가 1 또는 2로 주어진다.

출력

첫째 줄에 자두가 받을 수 있는 자두의 최대 개수를 출력한다.

예제 입력

7 2
2
1
1
2
2
1
1

예제 출력

6

해설

dp문제를 풀기 위해선(특히 bottom-up 방식) 꼭 dp테이블을 한번 생각하면서 그려보는 것이 굉장히 중요함을 깨닫게 되었다.

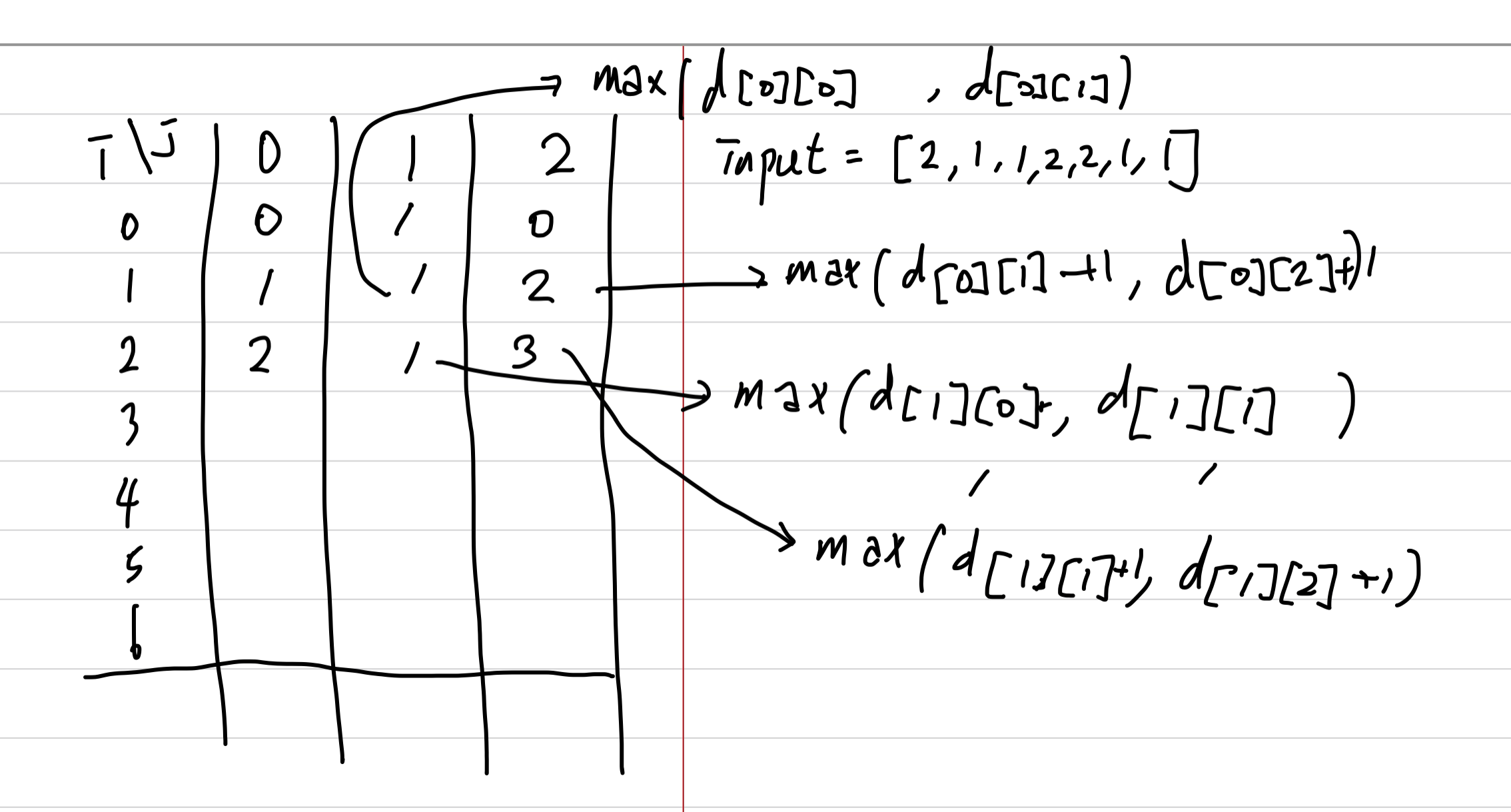
우선 d[i][j]의 테이블이 있고 i는 시간을, j는 총 움직인 횟수를 가리킨다. 즉 (j+1)%2 가 1이면 1번째 자두나무를, 0이면 2번째 자두나무에 있음을 가리킨다.

i가 0일때는 당연하게도 i초에서 떨어지는 자두에 따라 나누어 테이블을 정적으로 배치할 수 있다. 마찬가지로 j가 0일때는 i초까지 오는데 1번 자두나무에서 떨어진 횟수를 더해 구할 수 있다. 그러나 이것을 반복문 등으로 구현하기에는 시간복잡도가 너무 높아질 것 같아 d[i-1][0]에 i초때의 자두로 식별하여 1을 더하거나 더하지 않을 수 있다.

이해를 돕기 위한 표와 점화식은 다음과 같다.

제출 코드

import sys
t, w = map(int, sys.stdin.readline().strip().split())
trees = []
for i in range(t):
    trees.append(int(sys.stdin.readline().strip()))

# d[i][j]일때 i = 지나간 시간, j = 여태까지 움직인 횟수 그래서 d[i][j]는 i초일때 j만큼 움직여 얻을 수 있는 최대의 자두이다.
# 만약 7초라면 i인덱스는 6이다.
d = [[0 for _ in range(w+1)] for _ in range(t)]

for i in range(t):
    for j in range(w+1):
        if(i == 0):
            if(trees[i] == 1):
                d[i][j] = (j+1)%2
            else:
                d[i][j] = j%2
        elif(j == 0):
            if(trees[i] == 1):
                d[i][j] = d[i-1][j] + 1
            else:
                d[i][j] = d[i-1][j]
        else:
            if(trees[i] == 1):
                d[i][j] = max(d[i-1][j-1], d[i-1][j])+(j+1)%2
            else:
                d[i][j] = max(d[i-1][j-1], d[i-1][j])+(j)%2

print(max(d[t-1]))