ALGORITHM

[알고리즘] 하와이 가는 대학생

난이도

Silver 1

문제

하와와와… 대학생 라가는 ‘하와와’라는 말을 좋아하는 거시와요. 언제나 말 끝마다 ‘하와와’라고 말하는 라가는 자신이 좋아하는 하와와와 발음이 비슷한 하와이로 여행을 떠나기로 결심한 거시와요! 하와와와와… 그래서 라가는 구글 지도를 보면서 하와이 여행 계획을 세우고 있사와요…

하와이는 열도기 때문에, 라가는 열도들을 따라가면서 모든 섬을 여행하는 거시와요… 하와와와… 열도는 열을 따라 생겨 있는 섬이라는 뜻이고, 우리는 편의상 하와이의 섬 n개가 일렬로 배치되어 있다고 하는 거시와요… 이 때 첫 번째 섬에서 여행을 시작해야 하고, 열도를 여행하는 방법은 다음과 같이 세가지가 있는 거시와요…

어떤 섬을 보고 바로 그 다음 섬으로 갈 수 있사와요… 어떤 섬을 보고 한 섬을 건너뛰고 그 다음 섬으로 갈 수도 있사와요… 어떤 섬을 보고 그 이전 섬으로 갈 수 있사와요… 하와와.. 라가는 하와이의 모든 n개의 섬을 보고 싶은 거시와요… 또한, 라가는 지루함을 많이 타기 때문에 한번 갔던 섬에 다시 가고 싶지 않은 거시와요… 이 때, n개의 섬들이 있을 때 라가가 하와이를 여행하는 방법이 모두 몇 가지인지 구해 보는 거시와요…

하와와와… 그런데 저는 라가도 아닌데 왜 이런 말투를 쓰냐고요? 하와와 라가 친구쨩도 말투가 옮은 거시와요…

입력

첫째 줄에 하와이 열도의 섬의 개수 n(1 ≤ n ≤ 50,000)이 주어지는 거시와요 하와와. 하와와! 답이 커질 수 있으니 1,000,000,009로 나눈 나머지를 출력해 주시는 거시와요!

출력

첫째 줄에 라가가 여행할 수 있는 방법의 수를 출력하는 거시와요 하와와

예제 입력 

2

예제 출력 

1

해설 및 후기

정석적인 DP문제이다. 문제의 제목 때문에(실제 제목은 ‘하와와 대학생쨩 하와이로 가는 거시와요~’ 이다..) 무심코 들어가게 되었다. 여러 DP문제가 그렇듯, n을 늘려가며 실제로 한번 풀어보았다. 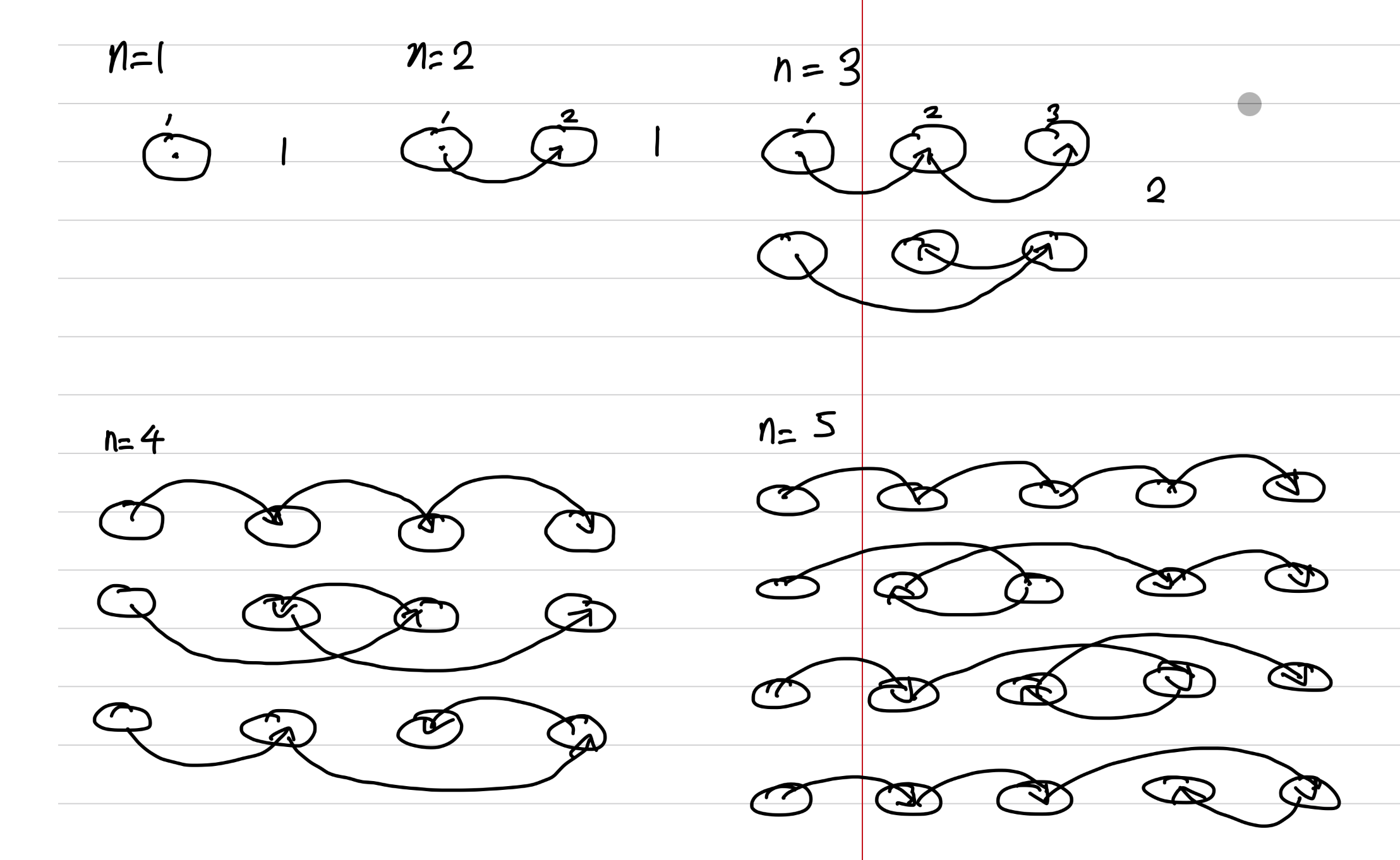값을 얻어내는 것 자체는 어렵지 않았는데, 어떻게 값을 도출해낼 수 있을까에 대한 고민을 하게 되었다. 이는 다른 방식으로 표현하면 더 쉽게 눈에 들어왔다.

문제에서 힌트를 얻어 그림으로 표현하는 것이 아닌 숫자로 표현하는 방식을 생각했다. 예를 들면 이런 식이다.

1을 전진, 2를 두칸 전진, -1을 후진이라고 했을 때,
n=1 이면 X
n=2 이면 1
n=3 이면 1, 1 | 2, -1
n=4 이면 1, 1, 1 | 1, 2, -1 | 2, -1, 2
...

즉 1, 2, -1을 조합해 n-1을 만드는 것과 동일한 문제가 된다. 그러나 여기에 더한 제한 조건이 있다.

  1. -1과 2는 연속으로 사용하지 못한다. (1은 가능)
  2. -1은 2의 다음에 사용할 수 있다. 2는 1과 -1의 다음에 사용할 수 있다.
  3. 1의 다음으로 2를 사용한다면 -1이 반드시 뒤에 붙는다.
  4. -1의 다음으로 2를 사용한다면 1이나 2를 뒤에 사용할 수 있다.

이를 종합적으로 고려하여 n=6의 케이스를 보자.

n=6 이면
1, 1, 1, 1, 1
2, -1, 2, 1, 1
1, 2, -1, 2, 1
1, 1, 2, -1, 2

2, -1, 2, [2, -1]
1, 1, 1, [2, -1]

총 이렇게 6케이스다. [2, -1]로 끝나는 경우를 따로 분류한 이유는 이것이 문제의 중요한 부분이기 때문이다.
[2, -1]로 끝나지 않는 경우를 살펴보면 n=6의 직전인 n=5에서 1혹은 2를 더하여 만들어진 케이스라는 것을 깨달을 수 있다.
반면 [2, -1]로 끝나는 경우는 여행이 무조건 n=6의 두번째 이전인 4번째에서 끝나는 경우와 횟수가 같다. n=4의 케이스와는 다르다. 3번째에서 끝나는 경우도 포함되어 있기 때문이다. 4번째에서 끝나는 경우의 횟수는 결국 n=3에서 1혹은 2를 더하여 만들어진 케이스이므로 n=3의 횟수와 완전히 동일하다.
즉 아주 간단한 점화식이 도출된다. dp[i] = dp[i-3]+dp[i-1] 이다. 미리 고심하고 푼 덕에 한번도 틀리지 않을 수 있었다. 앞으로도 이런 습관을 들여야겠다.

제출 코드 

n = int(input())
if(n <= 4):
    if(n == 1):
        print(1)
    else:
        print(n-1)
else:   
    dp = [0 for i in range(n+1)]
    dp[1] = 1
    dp[2:5] = [i-1 for i in range(2,5)]
    for i in range(5,n+1):
        dp[i] = (dp[i-3] + dp[i-1]) % 1000000009
    print(dp[n])