컴파일러의 구조
Phases of a compiler
- Lexial Analyzer : 상수 변수 이름들을 토큰별로 끊음. 변수 이름이 어디서부터 어디까진지 식별하며, 변수, 상수등의 정보를 담은 테이블인 Symbol table을 만듬. 이 과정이 끝나면 token stream을 내놓음.
- Syntax Analyzer : 문법에 잘 맞는지, 토큰과의 관계가 올바른지 검사한다. parser라고도 부름. 이 과정이 끝나면 syntax tree를 내놓음.
- Sementic Analyzer : 정수와 문자열의 덧셈이나 값을 0으로 나누는 등 의미적으로 올바르지 않은 항목이 있는지 검사함. 마찬가지로 이 과정이 끝나면 syntax tree를 내놓음.
- Intermediate code generator : 간단한 컴파일러들에선 생략됨. intermediate representation을 내놓음.
- Machine independent code optimizer : 간단한 컴파일러들에선 생략됨.
- Code generator : machine에 의존하는 기계어를 생성.
- Machine dependent code optimizer : machine마다 생성되는 기계어가 다르므로 코드 생성 이전과 이후 모두 optimize가 가능.
Transition of an assignment statement
position = inital + rate * 60
이러한 코드가 있다고 생각해보겠다. 아무런 컴파일 과정을 거치지 않은 상태에서는 전부 character이다.
1. Lexical Analyzer가 쭉 읽어가며 토큰을 나눔.
<token> : <id, 1> <=> <id, 2> <+> <id, 3> <*> <60>
과 같은 식으로 나누어지며, 이것이 token stream이다. 또한 Symbol table이 만들어지는데, 다음과 같은 식이다.
| 순서 | 제목 | 내용 |
|---|---|---|
| 1 | position | |
| 2 | initial | |
| 3 | table |
이후 만들어질 Syntax tree에는 변수명이 중요한 것이 아니라 변수의 유무가 중요하므로, 변수명을 사용하지 않는다.
2. Sytax Analyzer (parser)
다음은 완성된 Syntax tree이다.
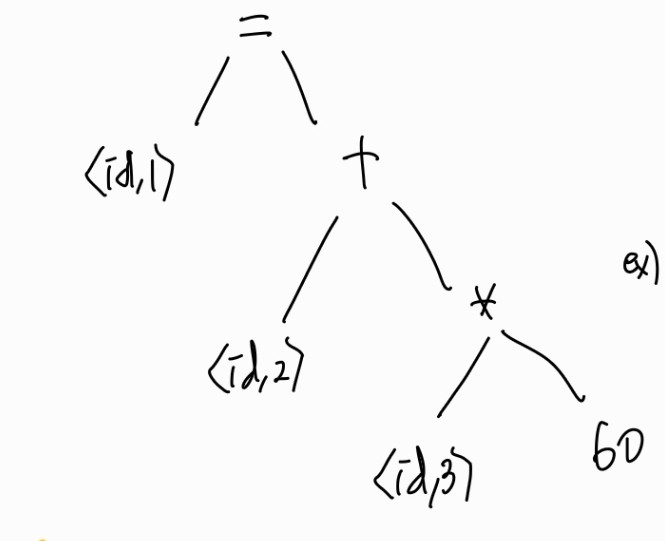
이렇게 Syntax tree가 올바르게 만들어지면 유효하다. 예를 들어, 연산자의 왼쪽에는 반드시 변수가 있어야 하는데 그게 아니라면 error가 발생하고, 우선순위를 고려할 수 있다.
3. Sementic Analyzer
위의 상황에서 position이 float라면, position에 int인 60을 대입하는 것은 의미적으로 옳지 않다. 따라서 자동으로 의미에 맞게 상수를 변형해주는 등의 역할을 수행한다. 그러면 Syntax tree의 일부분이 이렇게 개선된다.

4. intermediate code generator
internal node들에 이름을 부여한다.
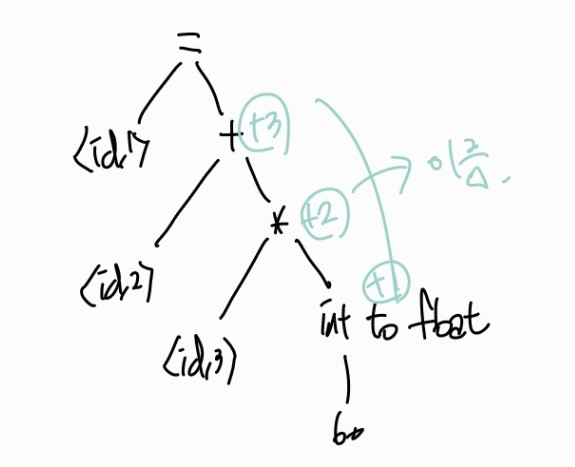
그러면 intermeddiate representation이 생기는데, 다음과 같은 식이다.
t1 = int to float
t2 = id3 * t1
t3 = id2 + t2
id1 = t3
복잡한 연산을 풀어내어 한 연산에 하나의 연산자를 사용한다. 기계어, 어셈블리어로 바꾸기 용이해지는 장점이 있다.
5. Code optimizer (machine independent)
t1 = id3 * 60.0
id1 = id2 + t1
이렇게 코드를 optimize할 수 있다.
6. Code generator
사용하는 CPU에 의존하는 코드가 생성된다. 예를 들어,
LDF R2, id3
MULF R2, R2, #60.0
LDF R1, id2
ADDF R1, R1, R2
STF id1, R1
이러한 방식으로 생성될 수 있으며, CPU마다의 의존이 다르기 떄문에, intermediate code 생성 이후 최적화할 수 있고, code gen이후에도 최적화할 수 있음.
7. Code optimizer (machine dependent)
아키텍쳐에 맞는 코드를 최적화한다.
intermediate representation
DAG(Directed Acyclic graph) for the expression
a + a * (b - c) + (b - c) * d 라는 연산이 있다면, 이에 대해
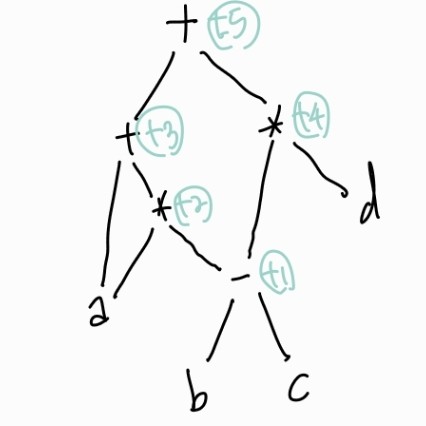
과 같은 이름이 부여된다. 이러한 형태는 이미 우선순위를 고려하여 만들어진 것이다. DFS Search 순서대로 넘버링이 붙는다.
Three-address code
오른쪽에 하나씩의 연산자만 붙는다. 이러한 코드를 DFS 순회하며 쓸 수 있다. (Postorder traversal 해야함. children이 먼저 eval되어야 하기 때문이다.)
그러면 위 tree를 code화 한 것은 다음과 같다.
t1 = b - c
t2 = a * t1
t3 = a + t2
t4 = t1 * d
t5 = t3 + t4
Quadruple representation
three-address code를 표현하는 또 다른 방법이다.
| op | arg1 | arg2 | result |
|---|---|---|---|
| - | b | c | t1 |
| * | a | t1 | t2 |
| + | a | t2 | t3 |
| * | t1 | d | t4 |
| + | t3 | t4 | t5 |
t1, t2…와 같은 변수들은 실제 기계어상에서 필요한 변수는 아니기때문에 최종적인 코드에서는 나타진 않음. (a,b,c,d는 필요) 추가적으로, grammer를 고려하면 자동으로 우선순위를 고려한 parser tree가 생성되게 된다!