A와 B를 languages라고 가정하면, A와 B 사이의 연산을 정의할 수 있다.

• Union : $A \cup B\,={x\mid x\in A$ $or$ $x\in B}$
• Concatenation : $A ° B$ $={xy\mid x \in A$ $and$ $y \in B}$
• Star : $A^*$ $={x_1x_2x_3…x_k\mid k\geq0$ $and$ $each$ $x_i\in A}$

예를 들어 {a,b,c,…,z}의 알파벳 set과 A = {good, bad}, B = {boy, girl}이 있다면,
$A \cup B$는 {good, bad, boy, girl}이고,
$A ° B$ 는 {goodboy, goodgirl, badboy, badgirl},
$A^*$는 {입실론, good, goodgood, goodbad, badgood, …}이다.

A, B가 regular language이면 A U B또한 regular language이다. 따라서 regular language 자체는 무한집합이다.

이를 증명하는 방법?

$Let \, M_1 = (Q_1,\sum,\sigma_1, q_1, F_1) \,and$
$M_2 = (Q_2,\sum,\sigma_2,q_2,F_2)$
편의상 사용하는 알파벳은 동일하다고 가정한다.

$L(M_1)=A\,and$
$L(M_2)=B$이면,

$construct \,M = (Q,\sum,\sigma,q,F)$ 그리고 그러한 M이
$L(M)=A \cup B$

즉 A와 B를 모두 accept하는 automaton을 만든다.

1. $Q = {(r_1,r_2)\mid r_1\in Q_1,r_2 \in Q_2}$ (즉, Q1과 Q2의 카티션 곱)
2. $\sum$은 M1, M2와 같다.
3. $For\,each\,(r_1,r_2)\in Q\,and\,each\,a\in\sum$
   $let \,\sigma((r_1,r_2),a) = (\sigma_1(r_1,a),\sigma_2(r_2,a))$ 즉 $r_1$에 대해서는 $\sigma_1$을 적용하고 $r_2$에 대해서는 $\sigma_2$을 적용해 새로운 페어를 형성한다.
4. $q_0=(q_1,q_2)$
5. $F={(r_1,r_2)\mid r_1\in F_1 \,or\,r_2\in F_2}$,즉 $(F_1\times Q_2)\cup(Q_1\times F_2)$

M은 하나의 오토마톤이지만, M1과 M2를 동시에 돌린다. 어떤 String이 A와 B 둘 중 하나에라도 속하면 Accept되며 어디에도 속하지 않으면 Reject한다.

Nondeterminism (NFA)

nondetermistic finite automaton인 N1을 정의한다.

NFA의 특징은 input에 따라 결정 가능한 state가 여러개일 수 있다는 것이고, empty string($\epsilon$)이 존재한다.

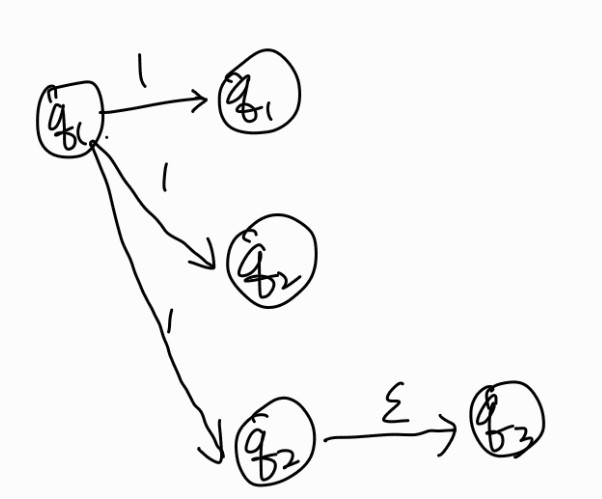
이는 더 파워가 큰 튜링에도 적용가능하다.(NTM)

이러한 N1에 대해, 문자열 010110이 입력되면 다음과 같이 작동한다.

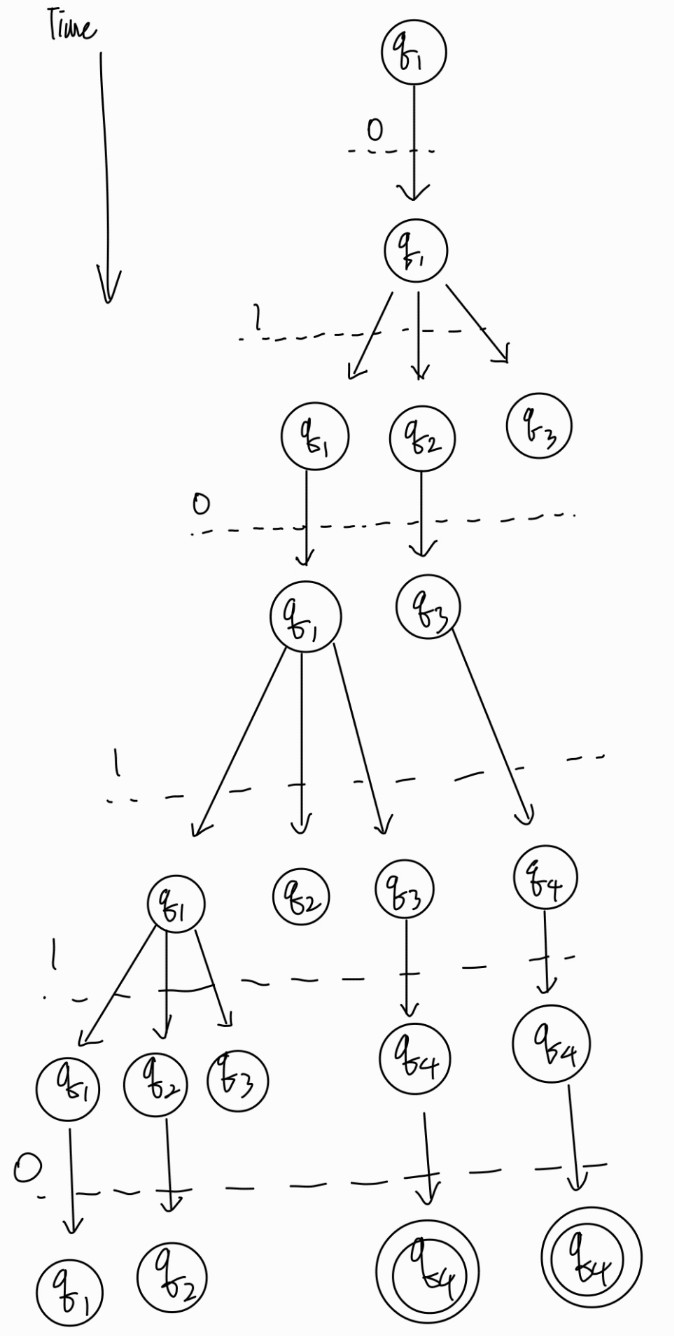
NFA의 경우 다양한 경우의 수가 가능하기 때문에, 마지막에 하나 이상의 state가 accept state가 된다면 accept처리된다. 즉 위의 예시인 010110은 accept되는 문자열이다.

Formal definiton of a NFA

DFA는 5개의 튜플을 가지고 있다. $(Q,\sum,\sigma,q_0,F)$

1. $Q$ : state
2. $\sum$ : Alphabet
3. $\sigma$ : $Q \times \sum_\epsilon \rightarrow P(Q)$ 전이함수. $\sum_\epsilon$이란 $\sum \cup {\epsilon}$을 의미하며, $P(Q)$는 $Q$의 파워 셋을 의미한다.
4. $q_0$ : start state
5. $F$ : set of accept state

DFA에 비해 $\sigma$부분만 바뀐 것을 알 수 있다. 일단 $\epsilon$의 사용이 가능해졌으므로 $\sum$에 $\epsilon$가 포함된 $\sum_\epsilon$를 사용하며, 같은 alphabet으로도 여러 state로 전이될 수 있으므로 power set of $Q$로 전이된다.

즉, $\sigma\, of\,DFA = Q\times\sum\rightarrow Q$이나
$\sigma\,of\,NFA = Q\times\sum_\epsilon\rightarrow P(Q)$이다.

예를 들어 $Q={q_0,q_1,q_2}$일때
$P(Q)={\phi, {q_0},{q_1},{q_2},{q_0,q_1},\dots,{q_0,q_1,q_2}}$ 이다.

그래서 위의 NFA를 Formal한 표현으로 정의하면

$N_1 = {Q,\sum, \sigma, q_1, F}$

$Q = {q_1,q_2,q_3,q_4}$
$\sum = {0,1}$
$\sigma =$

	0	1	$\epsilon$
$q_1$	${q_1}$	${q_1,q_2}$	$\phi$
$q_2$	${q_3}$	$\phi$	${q_3}$
$q_3$	$\phi$	${q_4}$	$\phi$
$q_4$	${q_4}$	${q_4}$	$\phi$

$q_1$은 start state
$F$ = ${q_4}$

다음은 0100, 11111처럼 끝에서 세 번째가 1인 string만 accept하는 automaton을 만들어보겠다.