Automaton 생성 예제와 DFA NFA 변환
조건에 맞는 Automaton 생성하기
$A = {0100,11111,01100,\dots}$ 처럼 뒤에서 세 번째가 1인 string만을 accept하는 automaton을 만들어 보자.
A를 인식하는 NFA
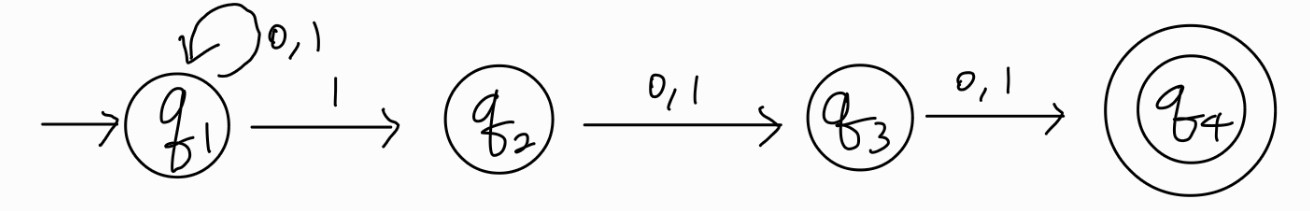
만약 0100이 들어온다면? $q_1$에서 끝날수도 있고 $q_4$에서 끝날수도 있다. 그러나 NFA는 하나라도 accept state로 끝나는 경우가 있다면 accept하다고 판단하므로 위 문자열은 accept.
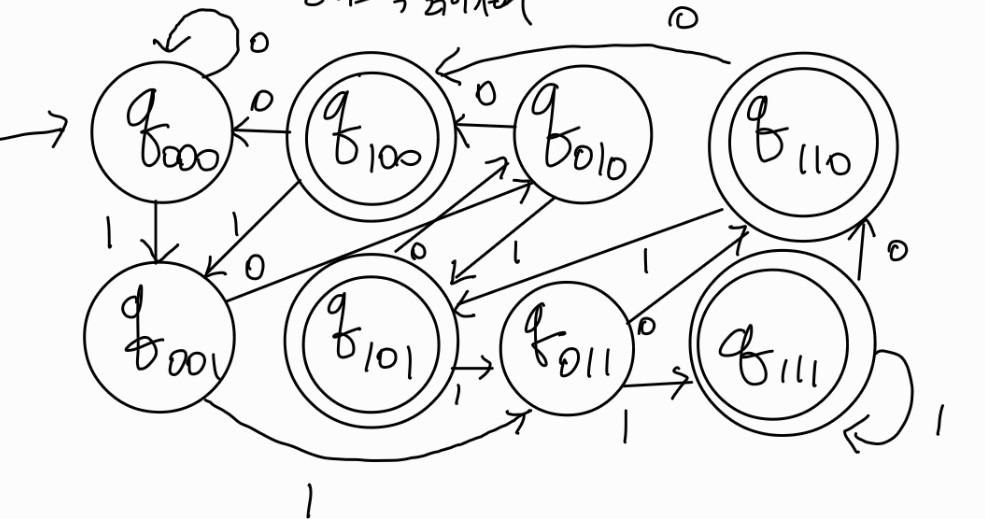
A를 인식하는 DFA
DFA는 NFA와 다르게 한 알파벳에 대해 한 state의 전이 경로만 존재할 수 있읍. 즉 state를 세 비트씩 할당하여, 100, 101, 110, 111으로 끝나게 되면 accept 하는 식으로 한다.
Let $A$ be the language consisting of all strings of the form $0^k$ where $k$ is a multiple of 2 or 3 including the empty string $\epsilon$
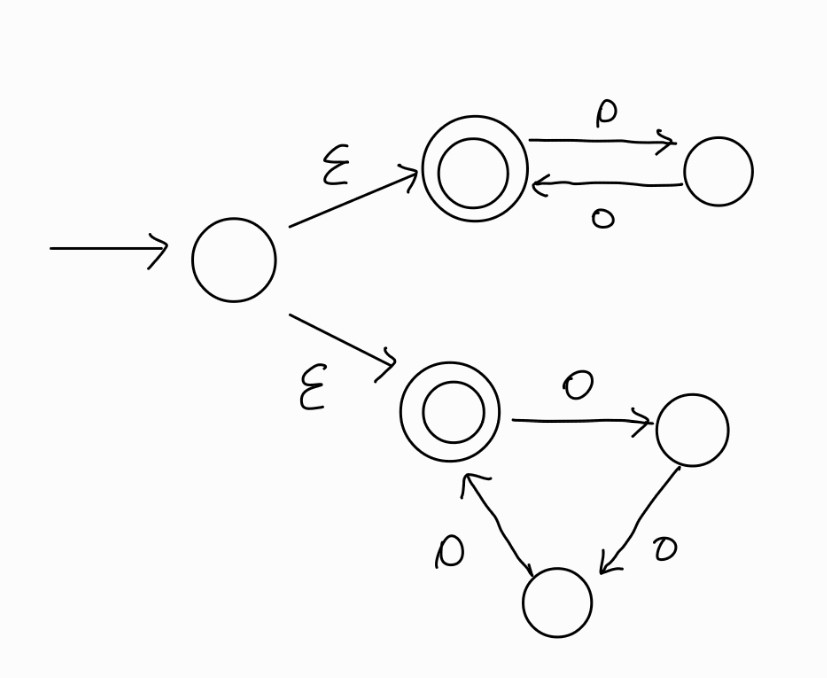
즉 $A={\epsilon,00,000,0000,000000,\dots,}$
다음과 같이 그릴 수 있다.
NFA와 DFA의 관계
모든 NFA는 equivalent DFA를 가지고 있다.
NFA의 경우, 하나의 알파벳에 여러 state가 가능하며, empty string $\epsilon$이 존재한다.
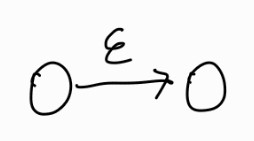
그러면 이러한 모양의 NFA를 DFA로 어떻게 변환할 수 있는가?
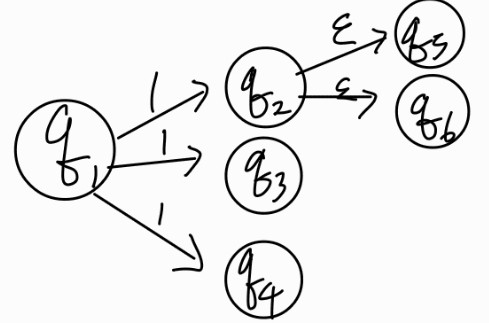
Power set을 정의해서, 갈수있는 모든 경우의 수를 생각한다.
예를 들어 다음과 같은 NFA N4가 존재한다면,
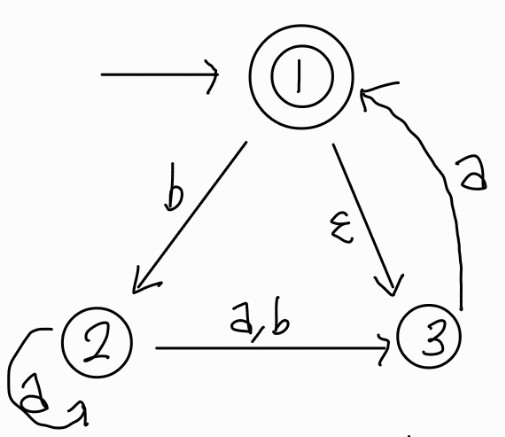
와 같은 NFA를
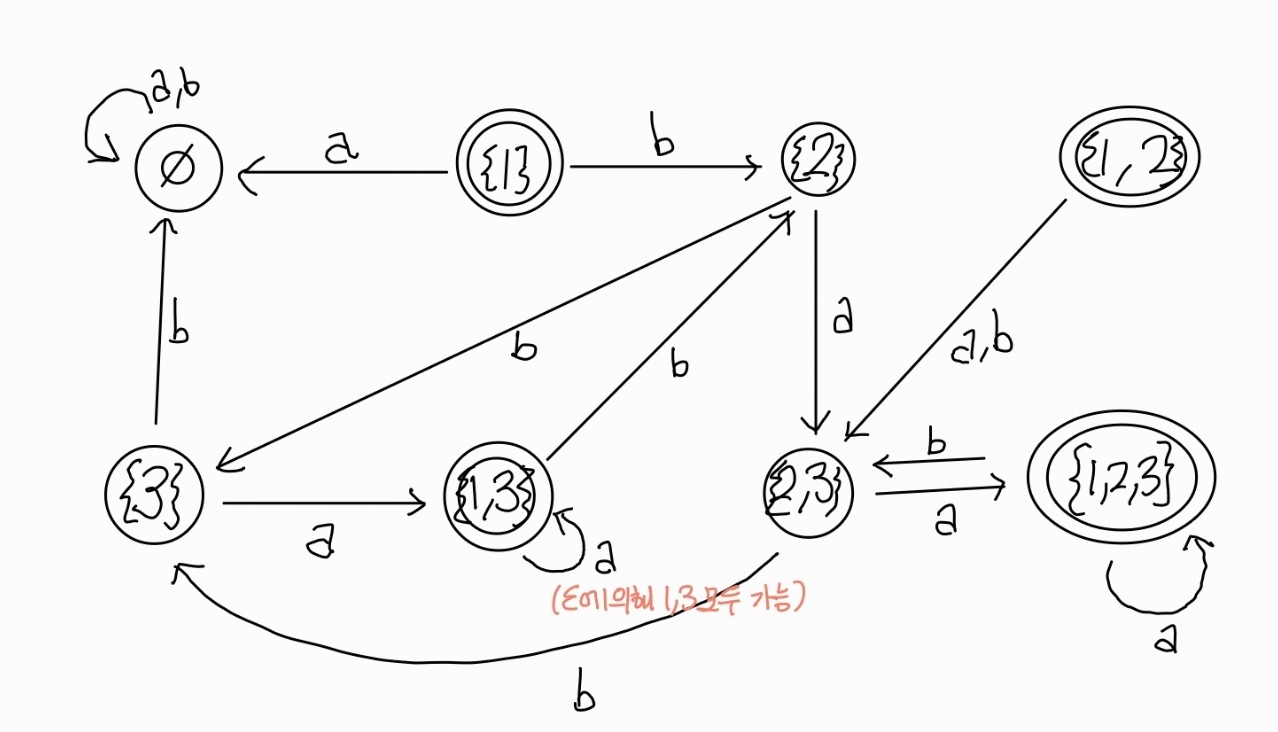
와 같이 표현할 수 있다. 시작점은 {1,3}이다. Accepting state를 포함하는 모든 power set을 accept state로 설정한다.