Every NFA has equivalent DFA

‘모든 NFA는 equivalent DFA가 존재한다’의 formal한 증명
$Proof, \,Let\,N=(Q,\sum,\sigma,q_0,F)\,be\,the\,NFA\,recognizing\,some\,language\,A$
이때 A를 인식하는 새로운 DFA $M=(Q’,\sum,\sigma’,q_0’,F’)$ 를 정의한다.

$Q’$ = $P(Q)$, power set of $Q$
$\sum$ = $N$의 $\sum$과 같음
$\sigma(R,a)’={q\in Q \mid q \in E(\sigma(r,a))\,for\,some\,r\in R}\, for\,R\in Q’\,and\,a\in\sum$
$q_0’=E({q_0})$
$F = {R \in Q’\mid R\,contains\,an\,accepting\,state\,of\,N}$

이때 $E(R)$이란, $M$의 어떤 state $R$에 대해서도 $\epsilon$화살표만 따라가서 R의 memeber로 도달할 수 있는 state의 집합이다.

만약 $w=0110$인 $w$를 $w=01\epsilon 1\epsilon 0\epsilon$처럼 쓸 수 있다.

레귤러 연산의 Formal한 표현

$L_1\cup L_2,\,L_1\circ L_2,\,L_1^*$
각각의 $L_1,\,L_2$가 regular이면 연산 후에도 regular이다. 즉, 그것을 Accept하는 NFA/DFA가 존재한다. 그림으로는 다음과 같이 그릴 수 있다.

$L_1\cup L_2$의 formal한 표현

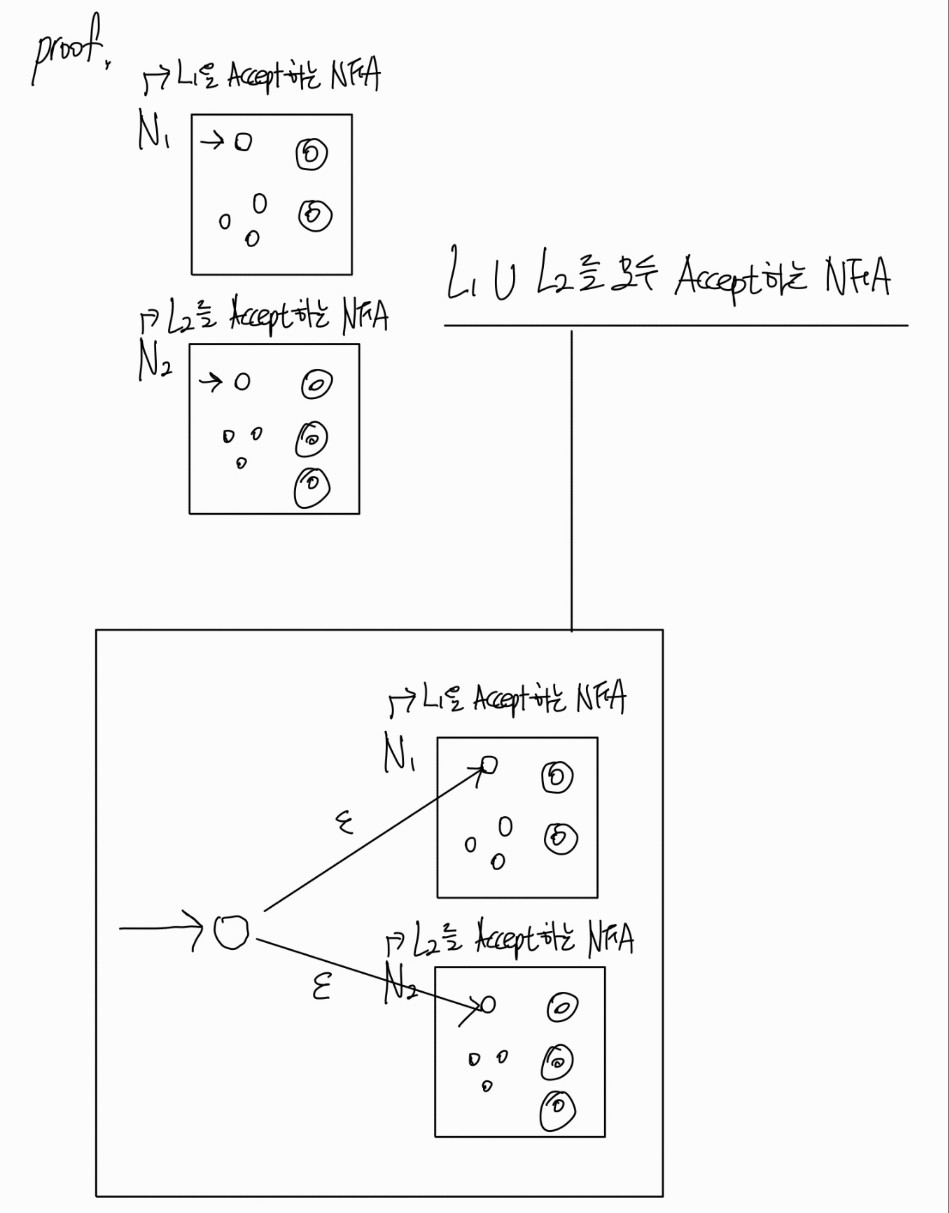
즉 $L_1\cup L_2$또한 regular하다. 이를 formal하게 표현해보겠다.

$Let\,N_1=(Q_1,\sum,\sigma_1,q_1,F_1)\, recognize\,A_1\,and$
$N_2=(Q_2,\sum,\sigma_2,q_2,F_2)\, recognize\,A_2.$

$Construct\,N=(Q,\sum,\sigma,q,F)$

$Q={q_0}\cup Q_1\cup Q_2$
$\sum$은 모두 같음
$\sigma=$
$\sigma_1(q,a),q\in Q_1$
$\sigma_2(q,a),q\in Q_2$
${q_1,q_2},a=\epsilon\,and\,q=q_0$
$\phi,a\neq \epsilon \,and\,q=q_0$
$q=q_0$
$F=F_1\cup F_2$

$L_1\circ L_2$의 formal한 표현

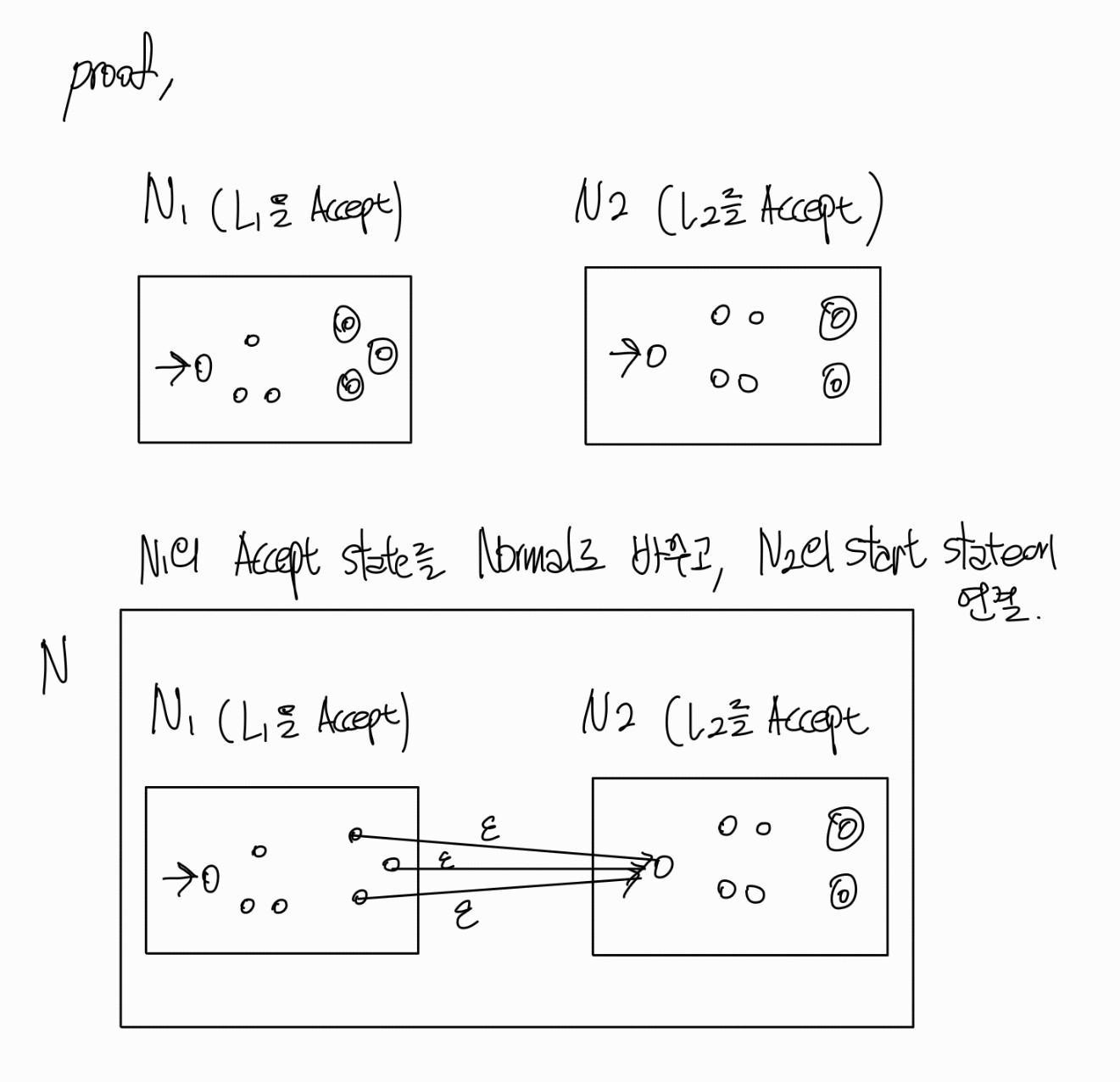
마찬가지로 $L_1\circ L_2$또한 regular하며 formal하게 표현해보겠다.

$Let\,N_1=(Q_1,\sum,\sigma_1,q_1,F_1)\,recognize\,A_1\,and$
$N_2=(Q_2,\sum,\sigma_2,q_2,F_2)\,recognize\,A_2$

$Construct\,N=(Q,\sum,\sigma,q,F)$

$Q=Q_1\cup Q_2$
$\sum$은 같음
$\sigma=$
$\sigma_1(q,a),q \in Q_1\,and\,q\notin F_1,$
$\sigma_2(q,a),q \in Q_2,$
$\sigma_1(q,a)\cup {q_2},q\in F_1\,and\,a=\epsilon,$
$\sigma_1(q,a), q\in F_1\,and\,a\neq \epsilon$
$q=q_1$
$F=F_2$

$L^*$의 formal한 표현

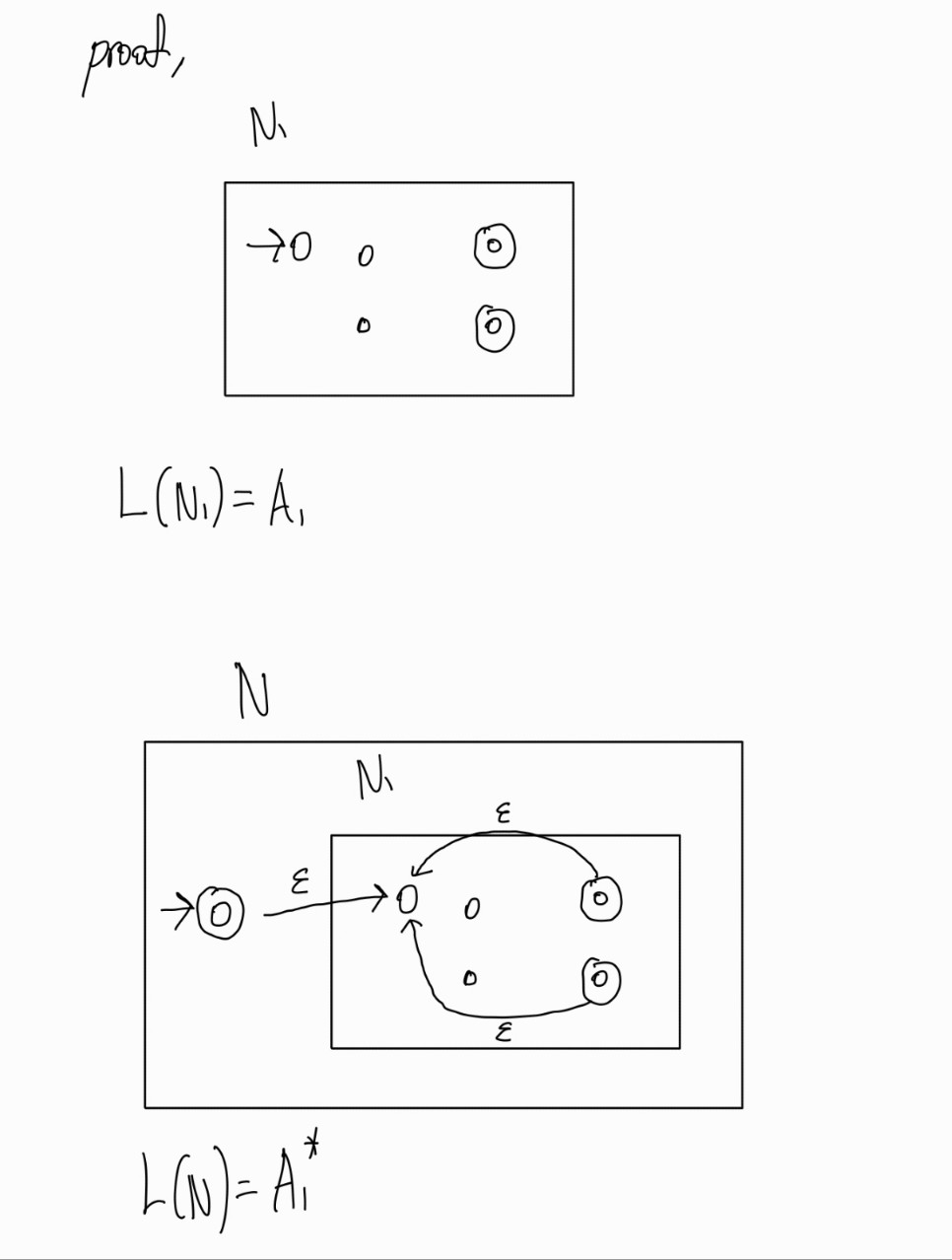
마찬가지로 $L^*$또한 regular하며 formal하게 표현해보겠다.

$Let\,N_1=(Q_1,\sum,\sigma_1,q_1,F_1)\,recognize\,A,$
$Construct\,N=(Q,\sum,\sigma,q,F)$

$Q={q_0}\cup Q_1$
$\sum$은 같음
$\sigma=$
$\sigma_1(q,a),q \in Q_1\,and\,q\notin F_1$
$\sigma_1(q,a)\cup {q_1},q \in F_1\,and\,a=\epsilon$
$q_1,q =q_0\,and\,a=ϵ$
$\sigma_1(q,a),q \in F_1\,and\,a \neq \epsilon,$
$\phi,q=q_0\,and\,a\neq \epsilon$
$q=q_0$
$F={q_0}\cup F_1$