regular expression의 정의

$R$은 이러한 조건을 만족하면 regular expression이라고 할 수 있다.

1. $a \in \sum$ 인 $a$만 가지고 있는 집합, $L(a)={a}$
2. $\epsilon$, $L(\epsilon)={\epsilon}$
3. $\phi$, $L(\phi)={}$
4. $(R_1 \cup R_2),$ $R_1$과 $R_2$가 모두 regular expression일 때.
5. $(R_1 \circ R_2),$ $R_1$과 $R_2$가 모두 regular expression일 때.
6. $(R_1^*),$ $R_1$이 regular expression일 때.

예를 들어 이러한 식들이 있다.

• $R^+ = RR^*$
• $R^* = R^+ \cup {\epsilon}$
• $(0 \cup \epsilon)(1 \cup \epsilon)={01,0,1,\epsilon}$
• $1^* \phi=\phi$
• $\phi^*={\epsilon}$
• $R \cup \phi = R$
• $R \circ \epsilon = R$

모든 regular한 language는 regular expression으로 정의할 수 있어야 한다.

예를 들면 $L(a*b)={b,ab,aab,aaab,\dots}$

그것을 증명해보도록 하겠다. R을 NFA인 N으로 변환시키면 이를 증명할 수 있다.

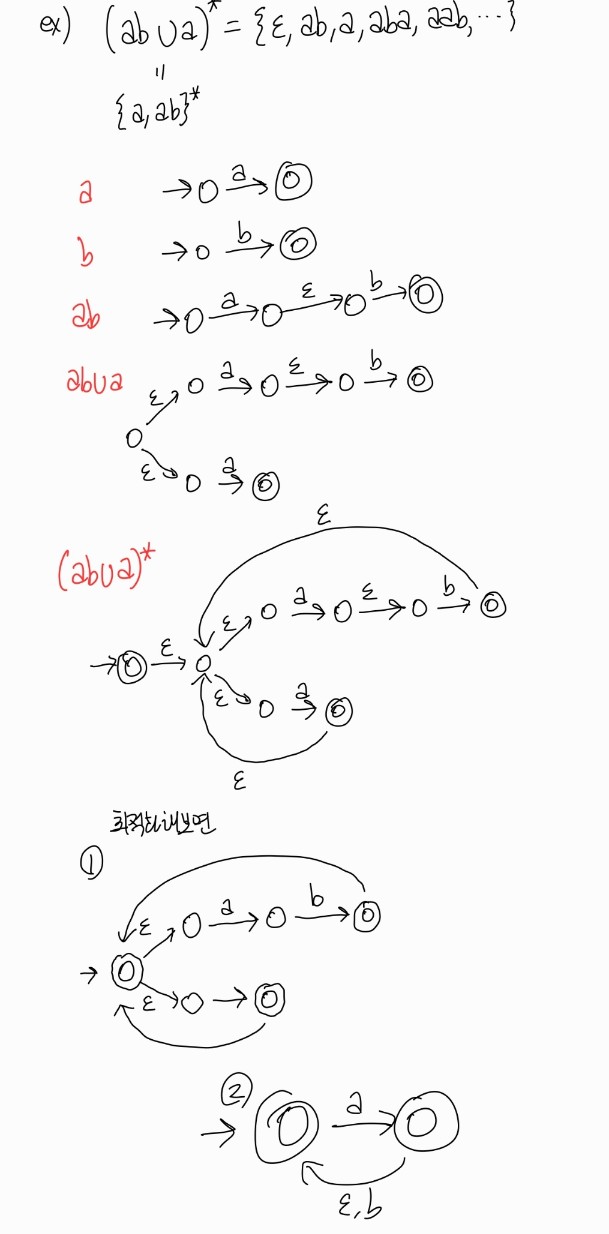
1. $R=a\,for\,some\,a\in \sum$
   그러면 $L(a)={a}$이다.
   이러한 NFA를 만드는 것은 간단하다.
   
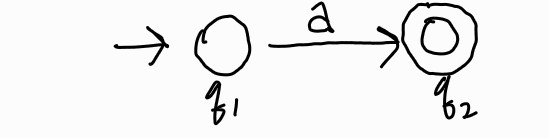
2. $R=\epsilon$
   그러면 $L(\epsilon)={\epsilon}$이다.
   
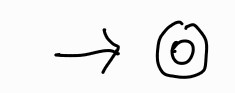
3. $R=\phi$
   그러면 $L(\phi)={}$이다.
   
4. $R=R_1 \cup R_2$
5. $R=R_1 \circ R_2$
6. $R=R_1^*$

4,5,6 번은 NFA가 R에 대해 닫혀있음을 증명한 구조처럼 가능하다.