Gauss Jordan Elimination 구현 (C++)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 | #include <iostream> #define sz 5 void printAugMtrx(double augMtrx[sz][sz+1], int size); void divAugMtrx(double augMtrxRow[sz + 1], int size, double op); void minAugMtrx(double toRow[sz + 1], double opRow[sz + 1], int size, double op); void rowCG(double augMtrx[sz][sz + 1], int size, int r1, int r2); void pivot(double augMtrx[5][6], int size); int main() { double mtrx[sz][sz+1] = { { 1.0, 7.0, 3.0, 2.0, 1.0, 49.0 }, { 2.0, 1.0, 2.0, 7.0, 2.0, 38.0 }, { 3.0, 2.0, 9.0, 4.0, 5.0, 50.0 }, { 7.0, 1.0,7.0, 1.0, 4.0, 44.0 }, { 9.0, 8.0,7.0, 6.0, 5.0, 102.0 }, }; printAugMtrx(mtrx, sz); pivot(mtrx, sz); } void printAugMtrx(double augMtrx[sz][sz+1], int size) { std::cout << "행렬 출력\n"; for (int i = 0; i < size; i++) { for (int j = 0; j < size+1; j++) { printf(" %4.3f ", augMtrx[i][j]); } std::cout << "\n"; } } void divAugMtrx(double augMtrxRow[sz + 1], int size, double op) { for (int i = 0; i < sz + 1; i++) { augMtrxRow[i] /= op; } } void minAugMtrx(double augMtrxRow[sz + 1], double opRow[sz + 1], int size, double op) { for (int i = 0; i < sz + 1; i++) { augMtrxRow[i] -= opRow[i]*op; } } void pivot(double augMtrx[sz][sz+1], int size) { //계수가 가장 큰 행을 구하기 for (int i = 0; i < sz; i++) { //각 열에 대해 피봇팅 double mx = augMtrx[i][i]; int mid = i; for (int j = i+1; j < sz; j++) { if (augMtrx[j][i] > mx) { mx = augMtrx[j][i]; mid = j; } } rowCG(augMtrx, sz, i, mid); std::cout << i+1<<"번째 pivot 수행.. \n"; for (int j = i; j < sz; j++) { divAugMtrx(augMtrx[j], sz + 1, mx); } for (int j = i + 1; j < sz; j++) { minAugMtrx(augMtrx[j], augMtrx[i], sz, augMtrx[j][i]); } printAugMtrx(augMtrx, sz); } std::cout << "상삼각행렬이 완성되었습니다. 후진대입법을 적용해 해를 구합니다.\n"; for (int j = sz - 1; j >= 0; j--) { for (int k = 0; k < j; k++) { minAugMtrx(augMtrx[k], augMtrx[j], sz, augMtrx[k][j]); } } printAugMtrx(augMtrx, sz); std::cout << "따라서 해당 연립방정식의 해는 ...\n"; for (int i = 0; i < sz; i++) { std::cout << "x"<<i+1<<" = "<<augMtrx[i][sz] <<"\n"; } } void rowCG(double augMtrx[sz][sz + 1], int size, int r1, int r2) { double tmp; for (int i = 0; i < sz + 1; i++) { tmp = augMtrx[r1][i]; augMtrx[r1][i] = augMtrx[r2][i]; augMtrx[r2][i] = tmp; } } | cs |
실행 결과
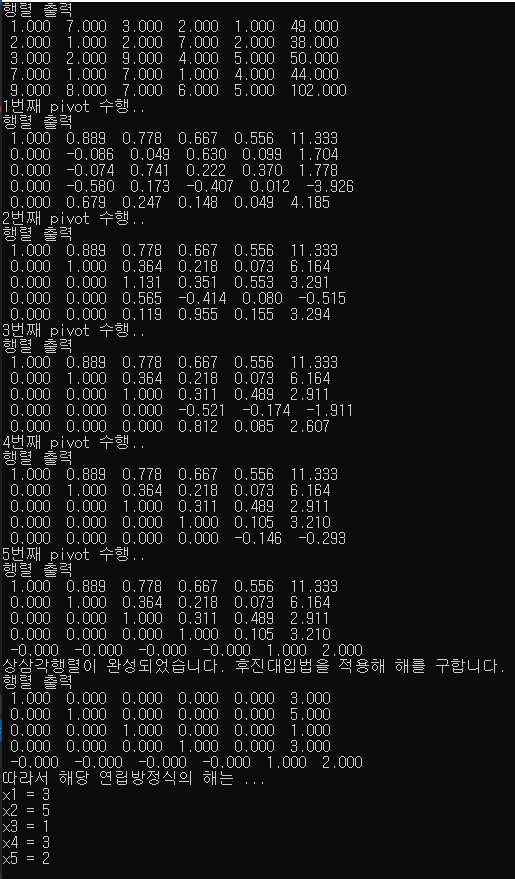
x1 = 3, x2 = 5, x3 = 1, x4 = 3, x5 = 2로 연립 방정식의 해를 구할 수 있었습니다.
후기
스크립트형 언어인 파이썬이나 매트랩을 사용했다면 훨씬 더 구현이 쉬웠을 것 같습니다. 행렬 계산과 관련된 부분이라 그러한 점이 더욱 체감되었습니다. 부동소수점 오차에 대해 개선해야 할 것 같습니다.